Top down Line of Sight

jaja1313

Hey everyone!

Firstly I believe in sharing my basic algorithms as it helps me with my thought process, it gives a starting point for beginners and it also gives the opportunity to others to partake in some constructive trashing.

I've been struggling for a while now to implement ( and remember my varsity calculus) a 2D top down line of sight algorithm. Basically something like this:


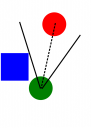
The Red unit is in the Green unit's view cone and is visible.

To determine if this is true I do:

1) Generate the normalized vector for the direction the Green Unit is looking
2) Subtract the Green Unit's position from the position of the Red Unit to get the direction vector to the object, and normalize that.
3) Calculate the dot product of these two vectors.

The dot product will give you the cosine of the angle between these two normal vectors. This will be 1 if the vectors point the same way, 0 if they are orthogonal, decreasing to -1 if they point in opposite directions. So you're looking for stuff that is close to 1.

Say you want your cone to be 30 degrees wide. So 15 degrees on each side of a line down the middle of the cone.

The cosine of 15 degrees is 0.969.

So if the dot product is greater than 0.969, then the object is within the cone. Otherwise, it's outside the cone.

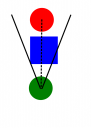
If we put an obstacle (for my game it is boxes) between the units, the above mentioned algorithm would still be true.



So once the Red unit is in the cone, I cast a ray from the Green Unit to the red. I loop through all obstacles and if that ray intersects any one of them I know the Red Unit is hidden!

...or is he:


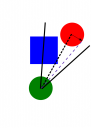
Here you can see that the ray intersects an obstacle, but a part of the Red Unit is still visible on Green's view cone.

WARNING!! Math to follow!
Green's position = Green.Pos
Red's position = Red.Pos

I'll have to test another 2 rays as well; Green.Pos to (Red.Pos +RightUnit.Vector(Red.Pos -Green.Pos). This would be the short arrow in the image. And do the same for the left unit vector.

If one of the three rays are not intersecting an obstacle, the Red Unit is visible.

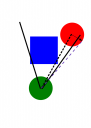
One last scenario:


Again the one ray hits an obstacle, the other is outside the view cone...

So I test with a ray down the edges of the view cone.

This is what I came up with, what do you think? What are the flaws and what can I improve on? Could this help any of you in any way?

Cheers

hermantulleken

One thing you should mention is what is the intent of the algorithm is. Is it for rendering optimisation? Is it for AI?

The reason that this is important is that you can take different shortcuts with different intents. For example, if it's for rendering optimisation, you can err on the side of sometimes rendering when you need not, for AI you could err on the side of missing sometimes when you should not. Either of these can simplify your algorithm.

jaja1313

OK, it is for AI.

Elyaradine

Um. Doesn't doing the raycasting pretty much do what you need out of the analytic approach? i.e., if the raycast (or spherecast or whatever) succeeds, then it's in your cone anyway? Just feels as if you're doing twice the work. (And I imagine it may be cheaper to fire a couple more rays for more accuracy than it'd be to be calling trig functions.)

And instead of doing the analytical bit, you could just create a mesh triangle, make it a trigger, parent that to the Green object, and check for whether things are within the trigger, instead of doing the maths. (I'm using Unity terminology, but I bet other engines would have similar stuff.)

Just saying that there might be easier (hackier? :P) ways to do this that might run better too, depending on what your goal is.

[edit] Oh. I have almost no experience with AI, so nvm. :D

dislekcia

No raycasting method, attack of the applied maths:

1. Construct list of obscuring objects and target objects within view cone. Sort both according to distance of closest point.

2. Build arc for the extents of each target object, scissoring against view cone extents. Test for triangle collision against obscuring objects. For each resulting collision, find arc extents of the obscuring object and construct new scissored arc of "remaining visible target area". Remove the object that just collided, test new arc against reduced list.

3. Either you will run out of arcs, in which case the object is not visible. Or you'll run out of obscuring objects to test against, meaning the object is visible. Note that you can sometimes have a collision that results in 2 arcs either side of a small obscuring object that's wholly contained by an initial arc test. Triangle collision is your friend, raycasting is not.

With raycasting and maximum sarcasm:

1. Same as above.

2. Calculate minimum "area" of target that needs to be visible for object to be seen. Slice up object into that many raycasts across the entire angle of the object inside the view cone. Do all of those casts against obscuring objects, if 1 of those doesn't collide with anything, object is visible.